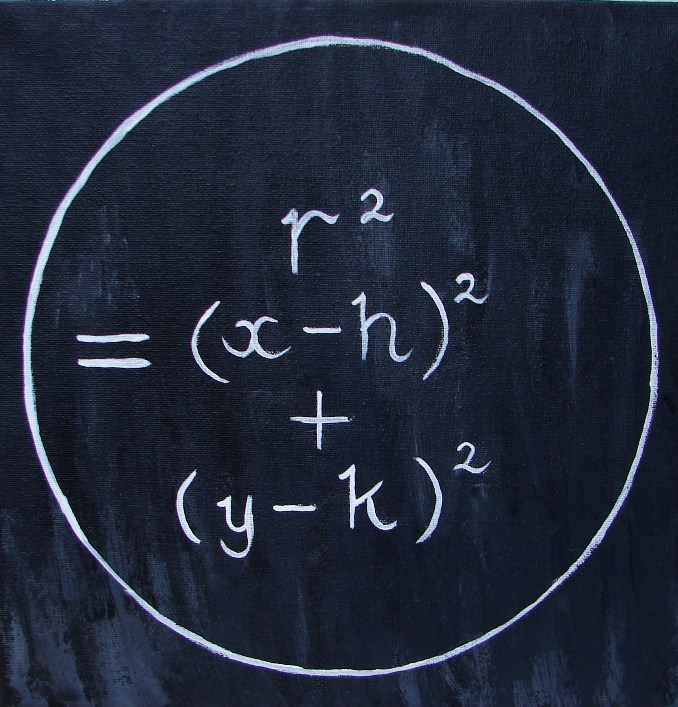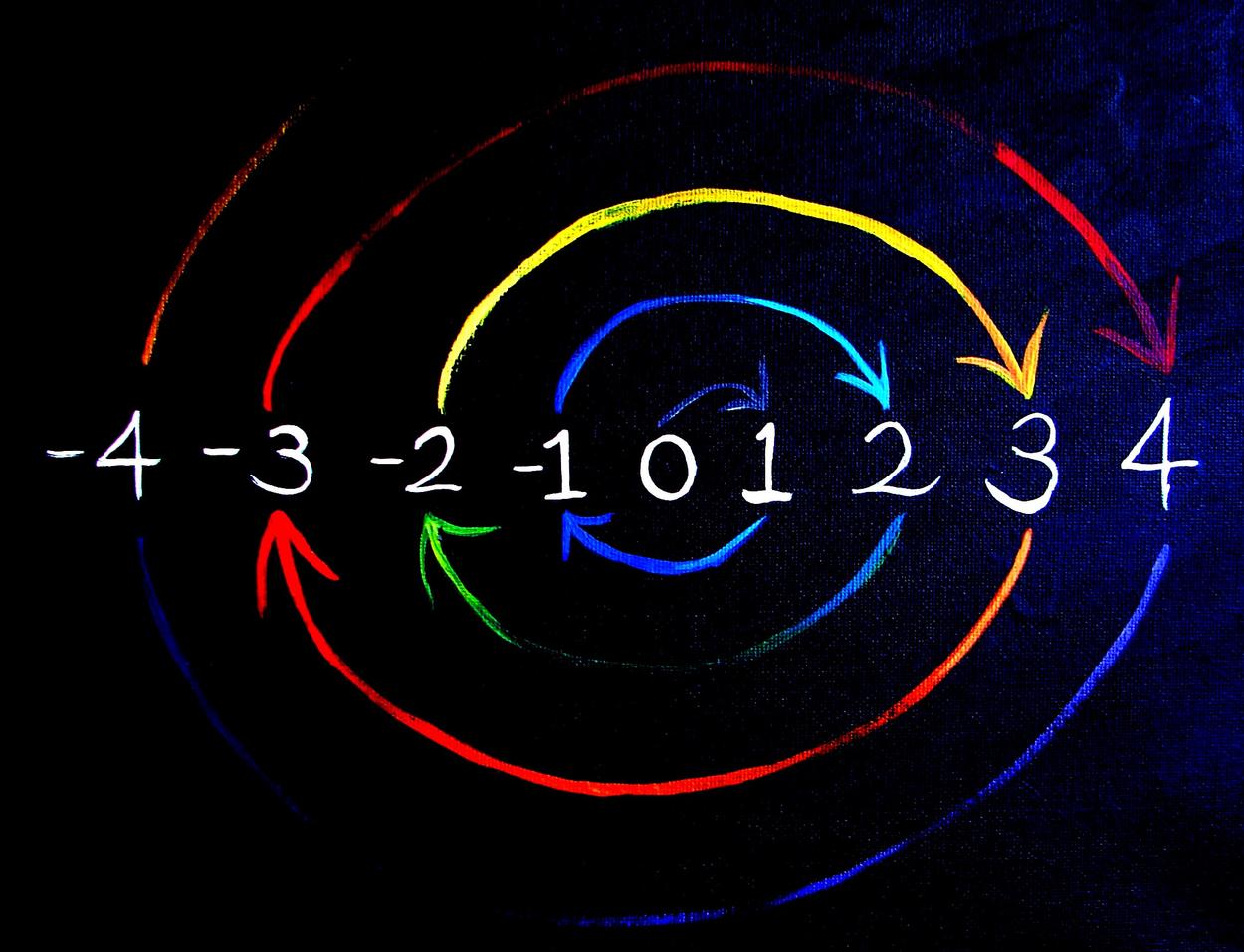Late in life, Newton said: 'I seem to have been only like a boy playing on the seashore, and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, while the great ocean of truth lay all undiscovered before me'.
William Blake took the mystic approach to the same concept: 'To see a World in a Grain of Sand// And Heaven in a Wild Flower// Hold Infinity in the palm of your hand// And Eternity in an hour'
Blaise Pascal expressed fear: 'The eternal silence of these infinite spaces terrifies me!'

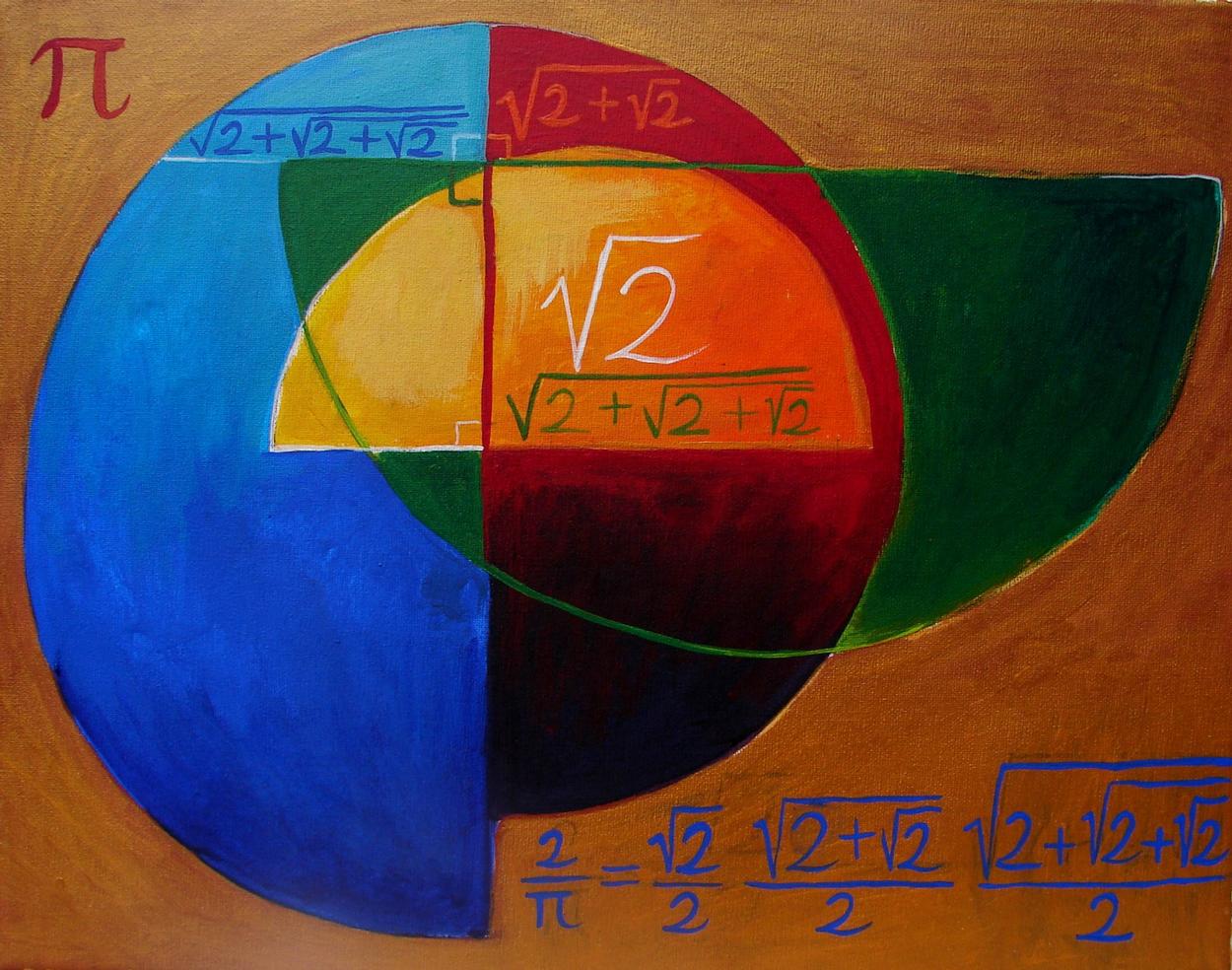
Years ago I was working on the ART OF LANGUAGE series, a series of paintings inspired by the languages of our world and concepts unique to those languages. While preparing a talk on the subject, I picked up a mathematical textbook. I wanted to illustrate the point that mathematics is not a language, just as musical notation is not a language.
The mathematician Robin Whitty was kind enough to give my paintings about mathematics a mention on his website and in truth he did warn me I might have some stray mathematicians coming my way...